Droga liczb

A co, gdyby matematyka wyższa z zadaniami o złożonych równaniach wielomianowych wysokiego stopnia i skomplikowaną geometrią była popularną sztuką i rozrywką dla samurajów, kupców, kobiet i nastolatków? A może nawet praktyką religijną? Sztuką, w której chodzi nie tylko o rozwiązanie poprawnie obliczeń, ale, aby rozwiązanie było piękne, harmonijne, wyrażało pewną myśl czy filozofię – jak haiku, albo ukiyo-e? Z pewnością taka matematyka nie byłaby aż tak praktyczna w naukach ścisłych, jak europejska - nie zbudowałaby mostów, ani samolotów. Ale, czy mogłaby w ogóle funkcjonować w taki sposób? Okazuje się, że tak – dziś poznamy matematykę wasan (和算) – japońską sztukę wyrafinowanych obliczeń matematycznych z okresu Edo (1603–1868) – matematykę w zamkniętym państwie, która wyewoluowała prawie całkowicie w separacji od reszty świata. Była pasją, rytuałem i intelektualną zabawą, której poziom dorównywał europejskim osiągnięciom XVII i XVIII wieku, a w niektórych przypadkach – wyprzedzał je o kilka dekad.

Na ruchliwych ulicach Edo, wśród kupieckich kramów i pachnących kadzidłami świątyń, wasan żyło w codzienności mieszkańców. W herbaciarniach mistrzowie kaligrafii i matematyki prowadzili gorące dyskusje nad zagadkami zapisanymi na cienkich drewnianych tablicach – sangaku (算額). Wyobraźmy sobie młodego samuraja, który w przerwie między treningami miecza mierzy się z zagadnieniem o wpisanych w figurę okręgach. Przesuwa drewniane patyczki (sangi), szukając harmonii w liczbach, a jego rywale – również kupcy i mnisi – przyglądają się w skupieniu. Może uda mu się znaleźć rozwiązanie tak piękne, że godne będzie pozostawienia w świątyni? W innym miejscu bogaty kupiec wiesza na chramie swoje sangaku, pokazując, że nie tylko w handlu, ale i w matematyce ma bystre oko. Być może gdzieś, w cieniu świątynnych filarów, młoda dziewczyna miko spogląda na problem zapisany staranną kaligrafią i w myślach szuka sposobu, by rozwiązać go lepiej niż jej ojciec? Bowiem, co dość nietypowe dla Japonii tamtych czasów, nie odsuwano kobiet od matematyki i mogły (o ile znały pismo) zgłębiać jej tajemnice.

Europejska matematyka rozwijała się w ścisłym związku z fizyką – Newton potrzebował rachunku różniczkowego, by opisać grawitację, Leibniz poszukiwał narzędzi do wyrażenia dynamiki świata. W Japonii wasan poszło inną drogą. Skupiało się na harmonii form, na wizualnej i konceptualnej elegancji. Dlatego też to w Japonii, na długo przed Europą, obliczono wartość liczby π z niespotykaną precyzją; to tu, w 1683 roku, Seki Takakazu odkrył determinat – matematyczne narzędzie, które w Europie zostało formalnie opisane dopiero dekadę później. To tu, w Japonii, pojawiły się metody rozwiązywania równań o stopniu sięgającym… 1458! Jeśli wasan miał swoją tajemnicę, to była nią nie tylko matematyczna precyzja, ale i połączenie nauki z pięknem. I choć ostatecznie Japonia przyjęła zachodnią matematykę w okresie meiji, wasan pozostaje fascynującym świadectwem epoki, w której liczby były nie tylko narzędziem – były sztuką.

Edo, miasto liczb – matematyczna codzienność Japonii

Słońce powoli wznosiło się nad Edo, barwiąc dachy drewnianych domów ciepłym, złotym światłem. Miasto budziło się do życia – ulicami płynęły strumienie ludzi, przekupnie zachwalali swoje towary, dźwięki kół drewnianych wózków i nawoływania handlarzy mieszały się w zgiełku poranka. Pachniało gotowanym ryżem, wędzoną rybą i kadzidłem unoszącym się znad świątyń. Był to świat pełen ruchu, rytuałów i codziennych zmagań, ale także świat liczb – bo Edo było miastem, w którym matematyka przenikała życie w zaskakujący sposób.

Na jednym z targowisk, w cieniu drewnianego zadaszenia, siedział sprzedawca tkanin, uważnie licząc na sorobanie – japońskim liczydle – należność za kupione przez klienta bele jedwabiu. Palce wprawnie przesuwały drewniane koraliki, niemalże instynktownie, a po chwili kupiec podniósł głowę i podał kwotę, nie mając cienia wątpliwości co do wyniku. Jego sąsiad, sprzedający herbatę, robił podobnie – obliczanie reszty było tu codziennością, ale w Edo nie chodziło tylko o rachunki. Liczby fascynowały ludzi. Nawet dziecko, które przyglądało się ojcu, bawiło się małym, podręcznym sorobanem, udając, że wykonuje obliczenia jak dorośli.

Nieco dalej, w jednej z herbaciarni, wśród parujących czarek i cichego szelestu kimon, toczyła się rozmowa między dwoma uczniami. Na stole leżał zwój pokryty starannie wykaligrafowanymi znakami i wykresami – to był problem matematyczny z ostatniej księgi wasan. „Jeśli masz dwa okręgi, które się przecinają, i wpiszesz w nie trzeci, jak wyliczysz jego promień?” – zapytał jeden z nich, stukając palcem w rysunek. Jego towarzysz uśmiechnął się i sięgnął po pędzelek. Z wprawą nakreślił kilka linii na kawałku papieru i zaczął objaśniać dowód. Kilku ciekawskich gości herbaciarni odwróciło się ku nim – rozmowy o matematyce były równie porywające jak opowieści o wojownikach i polityce (ale za to bardziej bezpieczne).

Jeszcze inna scena rozgrywała się na dziedzińcu świątyni. Wśród modlitewnych tabliczek ema wisiała ta jedna, wyjątkowa – sangaku, matematyczna zagadka zapisana na drewnianej desce. Kilku młodych uczniów, zafascynowanych problemem, szeptało między sobą, próbując znaleźć rozwiązanie. Stary mnich, który znał się na wasan, uśmiechnął się i podszedł bliżej. „To piękna zagadka” – powiedział, wskazując misternie wykaligrafowane wzory. – „Ale spójrzcie tu – czy nie wydaje się wam znajoma? Czyż to nie odmiana twierdzenia, które zapisano w księgach mistrza Seki Kōwa?” Uczniowie nachylili się bliżej, a ich umysły rozpalała pasja do nauki.

Wasan nie było tylko dziedziną dla wybranych. Na podwórzach domów w Edo dzieci rozwiązywały proste zagadki, licząc bambusowe kijki albo mierząc długości desek. W domach kupieckich młodzi adepci uczyli się wyznaczania procentów, by w przyszłości prowadzić rodzinne interesy. Nawet samuraje, którzy w czasie pokoju rzadziej sięgali po miecze, oddawali się zgłębianiu matematyki jako formy samodoskonalenia umysłu. Co więcej, choć kultura Edo nie była „przyjazna” kobietom, odmawiała im edukacji i możliwości stanowienia o sobie (bardziej lub mniej, wiadomo – wiele zależało i od prefektury i od rodziny, a także od samych jednostek), to jednak kobiety i młode dziewczęta bardzo często oddawały się rozrywce w psotaci wasan – rozwiązywania skomplikowanych zadań matematycznych i geometrycznych, których poziom współcześni matematycy określają jako „zaawansowana matematyka studiów wyższych XXI wieku”.

Edo było miastem, w którym liczby nie były abstrakcją – były częścią codziennego życia, sztuką, wyzwaniem i intelektualną zabawą. I nawet jeśli niektórzy nie dostrzegali w tym nic niezwykłego, to gdzieś w zaciszu świątyni, w herbaciarni lub na targowisku, ktoś właśnie odkrywał matematyczną prawdę, której Europa miała jeszcze nie poznać przez dziesięciolecia.

Choć to ostatecznie europejska (i później amerykańska) matematyka ukształtowała współczesną naukę, w XVII wieku rywalizacja między wasan a zachodnią myślą matematyczną nie miałaby jednoznacznego zwycięzcy. W odizolowanej Japonii rodziły się idee, które nie tylko dorównywały, ale czasem wręcz wyprzedzały osiągnięcia europejskich uczonych.

Czym jest wasan?

Kiedy w Europie matematyka stawała się narzędziem dla naukowców, inżynierów i filozofów przyrody, w Japonii epoki Edo wykształciła się jej wyjątkowa, niemal artystyczna odmiana – wasan (和算). Słowo to można przetłumaczyć jako „harmonijne obliczenia” lub po prostu „japońska matematyka”. „Harmonia” (和) nie jest tu przypadkowa – oznacza zarówno spokój i porządek, jak i odnosi się do Japonii jako kraju („Wa” oznaczało Japonię jeszcze przed „Nipponem” – więcej o tym piszemy tu: Dlaczego mówimy „Japan”, gdy Japończycy mówią „Nihon” – od Oyashimy do Zipangu, czyli zabawa w głuchy telefon przez tysiąclecia). Wasan było więc nie tylko systemem liczenia, ale także wyrazem narodowego ducha, sposobem myślenia i podejściem do nauki, które różniło się od europejskiego racjonalizmu znacząco.

Wasan a yōsan – dwie matematyczne ścieżki świata

Gdy Japonia otworzyła się na Zachód w epoce Meiji (1868–1912), matematyka europejska, określana jako yōsan (洋算, „zachodnie obliczenia”), szybko wyparła rodzime wasan. Dlaczego? Główna różnica polegała na podejściu do nauki.

Wasan rozwijało się niezależnie, odcięte od wpływów zachodnich aż do XIX wieku. Choć jego korzenie sięgały chińskich metod obliczeniowych, japońscy matematycy – zwłaszcza Seki Takakazu (Seki Kōwa) – nadali mu wyjątkowy charakter. Wasan stało się samodzielnym systemem matematycznym, w którym kluczową rolę odgrywała geometria.

Yōsan (matematyka europejska) rozwijało się w ścisłym związku z naukami przyrodniczymi – było narzędziem do opisu rzeczywistości i przewidywania zjawisk, od ruchu planet po dynamikę cieczy. Z kolei wasan nie miał tak ścisłych związków z fizyką czy astronomią, a jego rozwój podyktowany był głównie wewnętrzną fascynacją liczbami i formami.

Matematyczna sztuka – estetyka wasan

Jeśli w Europie matematyka była domeną uczonych, w Japonii była pięknem dostępnym dla każdego. Jednym z najbardziej niezwykłych aspektów wasan było to, że nie ograniczało się ono do elit naukowych – rozwiązywanie matematycznych zagadek było hobby zarówno dla samurajów, kupców, mnichów, jak i niekiedy, choć oczywiście rzadziej – bogatszych rolników. Dowodem na to są sangaku (算額) – drewniane tablice z geometrycznymi problemami, które wisiały w świątyniach i chramach, wystawione jako matematyczne ofiary dla bóstw.

Zadania w wasan często koncentrowały się na elegancji rozwiązania. Japońscy matematycy unikali skomplikowanych równań algebraicznych na rzecz harmonijnych konstrukcji geometrycznych, w których jedno twierdzenie wynikało naturalnie z drugiego. Z tego powodu wasan bywa porównywany do kaligrafii czy poezji – liczyło się nie tylko znalezienie odpowiedzi, ale sposób, w jaki została ona osiągnięta.

Matematyka codzienna rozrywka

Wasan przeniknęło japońskie społeczeństwo na poziomie niespotykanym w Europie. Było nie tylko domeną uczonych, praktycznym narzędziem w handlu, rolnictwie i administracji ale także – popularną rozrywką oraz formą sztuki. Znajomość liczenia była konieczna dla kupców, którzy musieli szybko obliczać ceny towarów, przewidywać zyski i straty, czy planować trasy transportowe. Również samurajowie, zarządzający finansami swoich lenn, musieli posługiwać się wasan na co dzień. Czym jednak wasan różniło się od zachodniej matematyki – było częścią ceremonii religijnych, były formą wyrazu uczuć (sztuka, zachwyt na harmonijnym pięknem) oraz rozrywką dla zarówno nastolatków, jak i dorosłych, którzy wcale nie byli bezpośrednio związani zawodowo z matematycznymi obliczeniami.

Z czasem wykształciły się nawet stopnie wtajemniczenia w wasan – od podstawowego poziomu, który obejmował cztery podstawowe działania, po zaawansowany poziom mistrzowski, na którym rozwiązywano problemy wymagające znajomości rachunku różniczkowego i całkowego (tak – istnieje japońska wersja tych metod obliczeń również!).

Co ciekawe, nie brakowało kobiet i dzieci, które pasjonowały się wasan. W dawnych Japonii nauka liczenia była jedną z niewielu dziedzin, w których mogły się rozwijać niezależnie od obowiązujących norm społecznych (czytaj: były dozwolone zarówno dla biedniejszej, choć umiejącej czytać, części społeczeństwa, a także dla kobiet).

Choć wasan ostatecznie ustąpiło miejsca zachodniej matematyce, jego wpływ na japońskie myślenie o liczbach i przestrzeni pozostaje nie do przecenienia. Nie było jedynie archaicznym systemem, lecz raczej alternatywną gałęzią matematycznej ewolucji, która podążyła własną drogą, rozwijając się równolegle do europejskiej nauki.

Do dziś w japońskich świątyniach można znaleźć zachowane sangaku, świadectwa epoki, w której matematyka nie była jedynie narzędziem, lecz sztuką – sztuką liczby, formy i harmonii.

Historia wasan

Początki: Chińskie korzenie i kalendarze niebios

Historia wasan zaczyna się jeszcze przed epoką Edo, w czasach, gdy Japonia czerpała inspiracje z nauki Chin. Już w okresie Nara (710–794) i Heian (794–1185) cesarski dwór gromadził chińskie teksty matematyczne, a uczeni próbowali dostosować tamtejsze metody do lokalnych potrzeb. Matematyka w tych czasach była ściśle związana z kalendarzami astronomicznymi – precyzyjne obliczenia były kluczowe dla określenia dat świąt, zaćmień i cykli księżycowych, które wpływały na rytuały religijne i rolnictwo.

Pierwsze samodzielne japońskie dzieła matematyczne pojawiły się później, w okresie Kamakura (1185–1333) i Muromachi (1336–1573). Były to teksty bazujące na chińskich modelach, ale zaczynały zawierać własne rozwiązania i interpretacje. Uważa się, że już wtedy sztuka liczenia zaczęła wykraczać poza potrzeby administracyjne czy religijne i przenikać do codziennego życia, zwłaszcza wśród kupców i urzędników samurajskich.

Złoty wiek wasan – matematyka epoki Edo (1603–1868)

Kiedy w 1603 roku władzę w Japonii przejęli Tokugawowie, kraj wszedł w erę pokoju i względnej stabilności. Edo stało się nie tylko politycznym centrum, ale także miejscem rozwoju nauki i sztuki. Właśnie wtedy matematyka wasan rozkwitła w pełni, wykształcając własną tożsamość i osiągając poziom porównywalny z europejskimi osiągnięciami matematycznymi.

To także epoka, w której powstawały szkoły i różne nurty matematyczne, a uczeni zaczęli tworzyć własne traktaty matematyczne – czasem tak zaawansowane, że przez lata nie były rozumiane nawet w Europie.

Seki Takakazu – geniusz niezależnej matematyki

Gdyby wasan miało swojego Newtona lub Leibniza, byłby nim Seki Takakazu (Seki Kōwa, 1642–1708). Ten niezwykły uczony, pochodzący z samurajskiej rodziny, zrewolucjonizował japońską matematykę i nadał jej nowy kierunek.

Był samoukiem, co samo w sobie było niezwykłe – zdobył wiedzę, studiując dostępne teksty, a następnie rozwinął ich myśl, wprowadzając własne, przełomowe metody. To on niezależnie odkrył determinat – kluczowy element algebry liniowej, który w Europie został opisany dopiero kilkanaście lat później przez Gottfrieda Leibniza. Stworzył też techniki, które przypominały rachunek różniczkowy, a jego uczniowie kontynuowali badania, które w teorii mogły doprowadzić kto wie do jakich przełomów matematycznych, gdyby nie izolacja Japonii.

Seki Takakazu zyskał tytuł „sansei” (算聖) – świętego matematyki, podobnie jak Sen no Rikyū był „świętym herbaty”, a Matsuo Bashō „świętym haiku”.

Matematyczne szkoły

Po Sekim w Japonii zaczęły powstawać szkoły matematyczne, które rozwijały różne aspekty wasan. Jego uczniowie i kolejni mistrzowie tworzyli traktaty matematyczne, w których formalizowali i poszerzali wiedzę. Wśród najważniejszych tekstów tego okresu można wymienić:

   → Hatsubi Sanpō („Podstawy matematyki”) – jedyna książka napisana przez Seki Takakazu,

   → Katsuyō Sanpō – zbiór matematycznych rozpraw jego uczniów

   → Jinkōki („Sztuka liczenia”) – najbardziej popularna książka matematyczna epoki Edo, autorstwa Yoshidy Mitsuyoshiego (1627).

Matematyka nie była już tylko domeną elit – kupcy, rzemieślnicy, mnisi, a nawet kobiety i dzieci zaczęli interesować się wasan jako formą rozrywki i ćwiczenia umysłu.

Sangaku – matematyczne wyzwania w świątyniach

Jednym z najciekawszych przejawów matematycznej kultury wasan były sangaku (算額) – drewniane tablice, na których zapisywano skomplikowane geometryczne zagadki i wieszano je w świątyniach i chramach.

Matematyka w Japonii miała bowiem duchowy wymiar – wielu uczonych traktowało liczby i figury geometryczne jako klucz do odkrywania porządku świata. Sangaku były formą matematycznej ofiary dla bóstw – jeśli ktoś znalazł piękne rozwiązanie problemu geometrycznego, zamiast zachować je dla siebie, przekazywał je świątyni jako dar.

Co ciekawe, autorami wielu sangaku byli zwykli ludzie – kupcy, rzemieślnicy, a nawet dzieci. Oznaczało to, że wasan stało się nie tylko sztuką elity, ale także powszechnym hobby, formą intelektualnego wyzwania i sposobem na spędzanie wolnego czasu.

Zmierzch wasan: epoka Meiji i zachodnia matematyka

Wszystko zmieniło się w drugiej połowie XIX wieku, kiedy Japonia otworzyła się na Zachód i rozpoczęła gwałtowną modernizację. Władze epoki Meiji (1868–1912) dążyły do jak najszybszego dorównania europejskim mocarstwom – także w nauce i edukacji.

Matematyka wasan, choć fascynująca i daleko rozwinięta, nie była dostosowana do nowoczesnych zastosowań. Nie wykorzystywano jej w fizyce, inżynierii czy astronomii, dlatego też została zastąpiona zachodnimi metodami, które lepiej nadawały się do rozwijania technologii.

W 1872 roku w japońskich szkołach wprowadzono obowiązkową naukę matematyki zachodniej, a tradycyjne wasan zaczęło odchodzić w zapomnienie. Nie oznaczało to całkowitego zaniku – do dziś niektóre szkoły kultywują tradycję sangaku, a badacze i miłośnicy historii matematyki w Japonii wciąż odkrywają na nowo tę niezwykłą epokę liczbowych eksperymentów.

Zasady wasan i różnice względem matematyki zachodniej

Filozofia i zastosowania wasan

Jedną z najbardziej uderzających cech wasan była jej całkowita odmienność filozoficzna od zachodniej matematyki. Podczas gdy w Europie w XVII wieku matematyka stawała się coraz bardziej narzędziem do opisu zjawisk fizycznych – czego najlepszym przykładem jest Isaac Newton, który stworzył rachunek różniczkowy do wyjaśnienia grawitacji – japońscy matematycy nie interesowali się naukami ścisłymi w takim sensie.

Wasan rozwijało się jako sztuka intelektualna, forma abstrakcyjnej gry umysłowej. Nie próbowano stosować jej do inżynierii czy nauk przyrodniczych – jej celem było doskonalenie umysłu oraz tworzenie pięknych i eleganckich rozwiązań geometrycznych.

Japońscy matematycy nie pytali: "Do czego możemy to zastosować?", lecz raczej: "Czy jest to eleganckie? Czy struktura tego dowodu jest piękna?". Stąd też tak wielką wagę przykładano do harmonii kształtów i symetrii – wyrażających się choćby w sangaku, czyli świątynnych tablicach z geometrycznymi łamigłówkami.

Wasan nie miało także zastosowań w ekonomii czy rachunkowości – w przeciwieństwie do matematyki europejskiej, rozwijanej m.in. przez Kartezjusza czy Pascala, którzy interesowali się teorią prawdopodobieństwa, analizą finansową czy mechaniką ruchu.

Wizualne podejście do matematyki – geometria jako sztuka

Wasan było oparte na geometrii, a figury matematyczne traktowano niemal jak kaligrafię – ważna była ich harmonia i estetyczna doskonałość.

Europejska matematyka w XVII-XVIII wieku coraz bardziej przechodziła na abstrakcyjny język algebry – rozwój rachunku różniczkowego, macierzy i liczb zespolonych prowadził do świata, w którym równania były coraz mniej związane z obrazowymi interpretacjami.

Wasan tymczasem pozostawało wierne geometrycznemu myśleniu – japońscy matematycy starali się rozwiązywać jak najwięcej problemów za pomocą proporcji, konstrukcji i wizualnych metod analizy. Łatwiej będzie nam sobie uzmysłowić tę inność w podejściu do matematyki dzięki poniższym przykładom:

   ∆   Problemy często dotyczyły kręgów wpisanych w trójkąty, stycznych i symetrii – figury były rysowane z dbałością o detale, a rozwiązania prezentowano w pięknej formie.

   ∆   Dowody miały nie tylko być poprawne, ale także "wizualnie satysfakcjonujące" – formę wyliczeń dostosowywano do tego, by wyglądały jak najbardziej harmonijnie.

   ∆   Sangaku nie były tylko zbiorami równań – ich rozmieszczenie i kompozycja były często dostosowane do estetyki świątyni, w której je umieszczano.

Współcześnie można by powiedzieć, że wasan było bliskie temu, co w XXI wieku określa się jako "matematyka wizualna" – stosowanie rysunków i intuicyjnych metod, zamiast suchego formalizmu algebraicznego.

Zastosowanie drewnianych patyczków (sangi) jako systemu obliczeń

Podczas gdy Europejczycy od XVII wieku rozwijali nowoczesną symbolikę algebraiczną (np. notację Kartezjusza dla równań czy Leibniza dla rachunku różniczkowego), Japończycy posługiwali się systemem sangi (算木) – drewnianych patyczków, które układano na specjalnych planszach w celu wykonywania obliczeń.

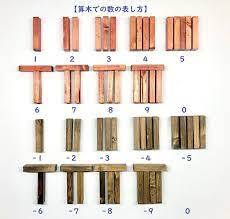
Jak działały sangi?

   ◊   Każdy patyczek symbolizował cyfrę – ich układ pozwalał przeprowadzać operacje matematyczne.

   ◊   System ten przypominał nieco rzymskie abakusy lub bardziej rozwinięte wersje liczydeł.

   ◊   Używano ich do dodawania, odejmowania, a także rozwiązywania układów równań – były szczególnie przydatne w obliczeniach geometrycznych i rachunku algebraicznym.

Sangi było jednym z powodów, dla których notacja algebraiczna wasan różniła się od zachodniej – zamiast równań pisanych w linii (np. y=3x+5), japońscy matematycy preferowali układy geometrycznych reprezentacji liczb.

Przykłady zaawansowanych osiągnięć wasan

Pomimo izolacji Japonii w epoce Edo, wasan osiągnęło wyniki, które w wielu przypadkach dorównywały, a czasem nawet wyprzedzały Europę.

Samodzielne odkrycie liczb Bernoulliego

Liczby Bernoulliego, czyli specjalna sekwencja liczb używana w analizie sumy potęg (np. 1k+2k+3k+...1^k + 2^k + 3^k + ...1k+2k+3k+...), zostały formalnie opisane przez szwajcarskiego matematyka Jakoba Bernoulliego w 1713 roku.

Jednak już rok wcześniej, w 1712, w Japonii Seki Takakazu i jego uczniowie zapisali ten sam wzór w traktacie „Katsuyō Sanpō”.

Dokładne przybliżenia liczby π

Wasan matematycy, stosując żmudne obliczenia przy pomocy metod geometrycznych i patyczków sangi, potrafili uzyskać dokładne przybliżenia liczby π (oczywiście, w japońskim nazewnictwie nie była to liczba „pi”, tylko: "en no hido" (円の比例), co można tłumaczyć jako "proporcja koła").

Takebe Katahiro (uczeń Seki Takakazu) obliczył wartość "en no hido” („pi”) do 41 miejsc po przecinku, co było jednym z najbardziej precyzyjnych wyników na świecie w XVIII wieku! (oczywiście „do 41 miejsc po przecinku” to taki skrót myślowy – Japończycy inaczej zapisywali takie liczby – jako szereg różnego rodzaju ułamków, nie jako: „3.1415927”).

Prace nad równaniami wielomianów wysokiego stopnia

Japońscy matematycy byli niezwykle ambitni – pracowali nad rozwiązywaniem równań algebraicznych o stopniu tak wysokim, że Europejczycy nie mieli jeszcze do nich metod. Jeden z matematyków wasan próbował znaleźć przybliżone rozwiązania równania algebraicznego 1458. stopnia – choć metody były inne niż w Europie, poziom trudności był imponujący.

Równania wielomianowe były rozwiązywane przy pomocy metod graficznych i wizualnych, bez użycia zachodnich wzorów analitycznych.

Twierdzenie o łańcuchu sfer Soddy’ego – 100 lat przed Zachodem

W 1936 roku brytyjski chemik Frederick Soddy opublikował w czasopiśmie Nature twierdzenie dotyczące sześciu kul wpisanych w przestrzeń między dwiema innymi kulami – tzw. twierdzenie o łańcuchu sześciu kul (albo lepiej: Soddy’s Hexlet Theorem).

Jednak japońskie dokumenty z 1822 roku zawierają dowód tego samego twierdzenia. Oryginalnie zostało ono zapisane w świątyni Samukawa przez Irisawę Shintarō Hiroatsu – kupca, który w wolnym czasie zajmował się wasan.

Sangaku – świątynne zagadki matematyczne

Czym były sangaku?

W cieniu drewnianych bram torii, pośród zapachu kadzideł unoszącego się w świątynnych dziedzińcach, wisiały niezwykłe tablice – sangaku (算額 – dosł. „tablica obliczeń”). Wykonane z drewna, ozdobione precyzyjnymi diagramami i zapisane eleganckimi znakami kanji, były czymś więcej niż zwykłymi ofiarami dla bogów. Były wyzwaniami rzuconymi innym umysłom, matematycznymi tajemnicami czekającymi na rozwiązanie.

Sangaku to geometryczne zagadki, które japońscy matematycy okresu Edo (1603–1868) ofiarowywali w świątyniach i chramach shintō. Nie były to jedynie formy modlitwy czy dowody wdzięczności – stanowiły również świadectwa intelektualnych osiągnięć ich twórców. Każda tablica zawierała problem, a często także jego rozwiązanie, wykaligrafowane misternie, jakby matematyka była sztuką kaligrafii. Przekaz był jasny: oto problem godny uwagi, oto dowód, że nasza wiedza i umiejętności w dziedzinie wasan mogą sięgać wyżyn ludzkiego poznania.

Dziś w Japonii zachowało się około tysiąca takich tablic. Niektóre z nich, wiszące w świątyniach przez setki lat, nadal skrywają nierozwiązane zagadki, które budzą podziw współczesnych badaczy.

Społeczna rola sangaku

Sangaku były czymś więcej niż tylko matematycznymi łamigłówkami – pełniły funkcję edukacyjną, społeczną i nawet religijną. Ich rozwiązywanie nie było wyłącznie domeną uczonych – do rywalizacji w tej niezwykłej dziedzinie włączali się samuraje, kupcy, rzemieślnicy, a nawet kobiety i dzieci. Była to intelektualna rozrywka dostępna dla każdego, kto miał dość cierpliwości i bystrości umysłu, by zmierzyć się z wymagającymi zagadkami.

W Japonii okresu Edo nauka matematyki nie była jedynie domeną elit – wasan rozwijało się w całym społeczeństwie, a świątynne tablice stanowiły zarówno sposób na popularyzację tej wiedzy, jak i narzędzie do demonstracji intelektualnej przewagi. Dla samurajów, którzy w czasie pokoju poszukiwali nowych dróg samodoskonalenia, sangaku stanowiły doskonałe wyzwanie. Kupcy widzieli w nich sposób na doskonalenie umiejętności niezbędnych w handlu, a dla uczonych były szansą na zapisanie się na kartach historii.

Sangaku spełniały także funkcję modlitewną – ofiarowanie nowej zagadki bóstwom świątynnym było formą duchowej wdzięczności za zdobyte umiejętności i nadzieją na dalsze oświecenie intelektualne. Matematyka i religia splatały się tutaj w wyjątkowy sposób, a rozwiązywanie trudnych problemów stawało się niemal aktem mistycznym.

Przykłady znanych zagadek

Tablice sangaku zawierały problemy geometryczne o różnym poziomie trudności – od prostych zadań dla początkujących po wyzwania, które nawet dziś wymagają zaawansowanych metod matematycznych.

Twierdzenie Pitagorasa w wersji wasan

Jeden z popularnych problemów sangaku przedstawia klasyczny przypadek trójkąta prostokątnego, ale w ujęciu specyficznym dla wasan. Na drewnianej tablicy można znaleźć skomplikowany diagram, w którym trójkąty prostokątne są układane w sposób przypominający origami, a ich zależności wyprowadzane za pomocą metod stosowanych w japońskiej matematyce.

Zagadki o wpisanych i opisanych okręgach

Typowe dla sangaku były również problemy dotyczące układów okręgów wpisanych i opisanych w trójkątach oraz innych wielokątach. Przykładem jest zadanie, w którym kilka współśrodkowych okręgów styka się ze sobą w skomplikowanym układzie – trzeba obliczyć ich promienie lub stosunek powierzchni.

Problemy o objętościach i polach powierzchni

Sangaku nie ograniczały się do płaskiej geometrii – niektóre zadają pytania o objętości brył, stosunki pól powierzchni czy sposoby podziału przestrzeni. Niektóre z tych zagadek są zadziwiająco bliskie temu, czym w Europie zajmował się Newton w swoich badaniach nad rachunkiem różniczkowym.

Niektóre z zagadek pozostają nierozwiązane do dziś. Być może ich autorzy celowo formułowali je w sposób, który wymagałby jeszcze większego wysiłku intelektualnego – lub też czekali, aż pojawi się ktoś godny, by je rozwikłać.

Dziś sangaku są cennym dziedzictwem kulturowym i matematycznym Japonii. Są dowodem na to, że matematyka w okresie Edo nie była tylko praktycznym narzędziem, lecz formą sztuki, pasją, a nawet sposobem na kontakt z boskością. I choć w epoce Meiji Japonia przyjęła zachodnią matematykę, świątynne tablice nadal pozostają świadectwem epoki, w której liczby i figury geometryczne mogły być czymś równie pięknym jak poezja czy malarstwo.

Zakończenie

Choć era wasan dobiegła końca wraz z modernizacją Japonii, jej duch wciąż żyje – zarówno w matematycznych zagadkach sprzed stuleci, jak i w nowoczesnych badaniach nad tą wyjątkową tradycją. Wasan było czymś więcej niż tylko matematyką – stanowiło intelektualne wyzwanie, rozrywkę, a nawet element duchowego życia społeczeństwa epoki Edo. Ożywiało świątynie dzięki sangaku, łączyło samurajów, kupców i uczonych w poszukiwaniu doskonałej harmonii liczb, a jego mistrzowie, jak Seki Takakazu czy Takebe Katahiro, odkrywali matematyczne prawdy równolegle do europejskich uczonych.

Dziś wasan nie jest już nauczane, a jego system notacji i metod rozwiązywania problemów pozostaje dla większości nieznany. Jednak współczesne technologie otwierają nowe możliwości w jego badaniu i zachowaniu. Cyfrowe archiwa pozwalają przechować setki dawnych ksiąg matematycznych, a narzędzia sztucznej inteligencji, oparte na deep learning, rewolucjonizują sposób, w jaki analizujemy historyczne dokumenty. Szczególnym wyzwaniem pozostaje rozpoznawanie kanji, które przez stulecia zmieniły swój wygląd, co utrudnia ich automatyczną klasyfikację i transkrypcję.

Jednak problemem nie są tylko techniczne trudności. Badania nad wasan stoją przed większym zagrożeniem – starzeniem się kadry badawczej i brakiem następców. Coraz mniej uczonych zajmuje się tą dziedziną, a jeśli nie podejmiemy działań, ryzykujemy utratę cennej części japońskiego dziedzictwa intelektualnego. Kluczowym zadaniem na przyszłość jest tworzenie otwartych baz danych, narzędzi edukacyjnych i popularyzacja wasan, aby ocalić je dla kolejnych pokoleń.

Bo choć historia wasan zakończyła się w szkołach Meiji, japońska matematyka wciąż ma szansę przetrwać – w cyfrowym świecie, gdzie liczby nie znają granic czasu.

Sprawdź podobne artykuły:

Japońscy artyści kontra cenzura shogunatu Edo: Jak Kuniyoshi w obrazie „Czarownica Takiyasha” krytykował władzę

Shogun wprowadza prawo ochrony zwierząt przed okrucieństwem w XVII wiecznej Japonii Edo

Ninja na emeryturze - co się działo z Shinobi w czasach pokoju Edo?

Co zrobić ze społeczeństwem samurajów znających tylko wojnę i śmierć w czasach pokoju? - sprytne pomysły shogunów Tokugawa

Kabukimono, tęskniąc za wojną – wolni indywidualiści, morderczy awanturnicy i szaleńcy w damskich kimonach

    未開    ソビエライ

  Mike Soray

   (Michał Sobieraj)

未開    ソビエライ

 Pasjonat kultury azjatyckiej z głębokim uznaniem dla różnorodnych filozofii świata. Z wykształcenia psycholog i filolog - koreanista. W sercu programista (gł. na Androida) i gorący entuzjasta technologii, a także praktyk zen i mono no aware. W chwilach spokoju hołduje zdyscyplinowanemu stylowi życia, głęboko wierząc, że wytrwałość, nieustający rozwój osobisty i oddanie się swoim pasjom to mądra droga życia. Autor książki "Silne kobiety Japonii" (>>zobacz)

Osobiste motto:

"Najpotężniejszą siłą we wszechświecie jest procent składany." - Albert Einstein (prawdopodobnie)

Mike Soray

(aka Michał Sobieraj)

Napisz do nas...

Ciechanów, Polska

dr.imyon@gmail.com

___________________

inari.smart

Chcesz się podzielić swoimi przemyśleniami czy uwagami o stronie lub apce? Zostaw nam wiadomość, odpowiemy szybko. Zależy nam na poznaniu Twojej perspektywy!